Creating vectorial isobands with Python

GDAL has an utility program, gdal_contour, that generates contour lines from a raster file (take a look at his example post). GDAL provides access to this method through its API, so contour lines can be generated inside your GDAL python scripts.

Unfortunately, there is no way to generate isobands, that is, filled contour lines that use polygons instead of polylines. Creating isobands allows the creation of nice contour maps easily, colouring the zones between two values:

 

 

Using contour lines, the result is this one:

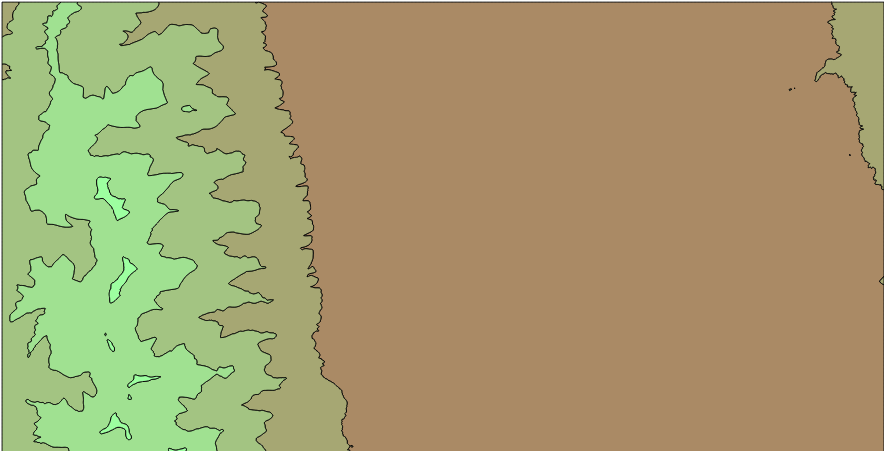
Both visualizations are drawn directly from QGIS.

So I created two scripts to get the result. As usual, you can download them from my GitHub account.
I created two scripts, since the one I like the most uses matplotlib, so sometimes it's not convenient to install. On the other hand, the other has less requirements (GDAL python), but the code is dirtier.

Both have the same usage, which is very similar to the gdal_contour usage:

    Usage: isobands_matplotlib.py [-h] [-b band] [-off offset] [-i interval]
    [-nln layer_name] [-a attr_name] [-f formatname]
    src_file out_file
    Calculates the isobands from a raster into a vector file

    positional arguments:
      src_file         The raster source file
      out_file         The vectorial out file
    optional arguments:
      -h, --help       show this help message and exit
      -b band          The band in the source file to process (default 1)
      -off offset      The offset to start the isobands (default 0)
      -i interval      The interval (default 0)
      -nln layer_name  The out layer name (default bands)
      -a attr_name     The out layer attribute name (default h)
      -f formatname    The output file format name (default ESRI Shapefile)

Just choose the input and output files, the input file band to process (1 by default), and the interval, and you will get the  vector file in the GIS format of your choice.

Now, the code of both script, step by step.

isobands_matplotlib.py

As it's name suggests,  this version uses matplotlib, and more specifically the contourf function, to create the isobands.

The script has a function called isobands, that actually generates the data, and a main part that reads the user input values:

if __name__ == "__main__":

    PARSER = ArgumentParser(
        description="Calculates the isobands from a raster into a vector file")
    PARSER.add_argument("src_file", help="The raster source file")
    PARSER.add_argument("out_file", help="The vectorial out file")
    PARSER.add_argument("-b", 
        help="The band in the source file to process (default 1)", 
        type=int, default = 1, metavar = 'band')
    PARSER.add_argument("-off", 
        help="The offset to start the isobands (default 0)", 
        type=float, default = 0.0, metavar = 'offset')
    PARSER.add_argument("-i", 
        help="The interval  (default 0)", 
        type=float, default = 0.0, metavar = 'interval')
    PARSER.add_argument("-nln", 
        help="The out layer name  (default bands)", 
        default = 'bands', metavar = 'layer_name')
    PARSER.add_argument("-a", 
        help="The out layer attribute name  (default h)", 
        default = 'h', metavar = 'attr_name')
    PARSER.add_argument("-f", 
        help="The output file format name  (default ESRI Shapefile)", 
        default = 'ESRI Shapefile', metavar = 'formatname')
    ARGS = PARSER.parse_args()

    isobands(ARGS.src_file, ARGS.b, ARGS.out_file, ARGS.f, ARGS.nln, ARGS.a, 
        ARGS.off, ARGS.i)

I used the argparse.ArgumentParser to read the script arguments, since is easy to use and it should come woth most of the updated python distributions (since python 2.7, I think).
This part of the code is quite easy to understand, it simply sets the arguments with their default value, sets if they are mandatory or not, etc.

The isobands function creates the vector file:

def isobands(in_file, band, out_file, out_format, layer_name, attr_name, 
    offset, interval, min_level = None):
    '''
    The method that calculates the isobands
    '''
    ds_in = gdal.Open(in_file)
    band_in = ds_in.GetRasterBand(band)
    xsize_in = band_in.XSize
    ysize_in = band_in.YSize

    geotransform_in = ds_in.GetGeoTransform()

    srs = osr.SpatialReference()
    srs.ImportFromWkt( ds_in.GetProjectionRef() )  

    #Creating the output vectorial file
    drv = ogr.GetDriverByName(out_format)

    if exists(out_file):
        remove(out_file)
    dst_ds = drv.CreateDataSource( out_file )
       
    dst_layer = dst_ds.CreateLayer(layer_name, geom_type = ogr.wkbPolygon, 
        srs = srs)

    fdef = ogr.FieldDefn( attr_name, ogr.OFTReal )
    dst_layer.CreateField( fdef )



    x_pos = arange(geotransform_in[0], 
        geotransform_in[0] + xsize_in*geotransform_in[1], geotransform_in[1])
    y_pos = arange(geotransform_in[3], 
        geotransform_in[3] + ysize_in*geotransform_in[5], geotransform_in[5])
    x_grid, y_grid = meshgrid(x_pos, y_pos)

    raster_values = band_in.ReadAsArray(0, 0, xsize_in, ysize_in)

    stats = band_in.GetStatistics(True, True)
    if min_level == None:
        min_value = stats[0]
        min_level = offset + interval * floor((min_value - offset)/interval)
   
    max_value = stats[1]
    #Due to range issues, a level is added
    max_level = offset + interval * (1 + ceil((max_value - offset)/interval)) 

    levels = arange(min_level, max_level, interval)

    contours = plt.contourf(x_grid, y_grid, raster_values, levels)

    

    for level in range(len(contours.collections)):
        paths = contours.collections[level].get_paths()
        for path in paths:

            feat_out = ogr.Feature( dst_layer.GetLayerDefn())
            feat_out.SetField( attr_name, contours.levels[level] )
            pol = ogr.Geometry(ogr.wkbPolygon)


            ring = None            
            
            for i in range(len(path.vertices)):
                point = path.vertices[i]
                if path.codes[i] == 1:
                    if ring != None:
                        pol.AddGeometry(ring)
                    ring = ogr.Geometry(ogr.wkbLinearRing)
                    
                ring.AddPoint_2D(point[0], point[1])
            

            pol.AddGeometry(ring)
            
            feat_out.SetGeometry(pol)
            if dst_layer.CreateFeature(feat_out) != 0:
                print "Failed to create feature in shapefile.\n"
                exit( 1 )

            
            feat_out.Destroy()

• Lines 26 to 49 open the input file and create the output vector file.
• Lines 53 to 57 set two matrices, containing the coordinates for each pixel in the input file. To do it, two vectors are created first with the coordinates calculated from the input geotransform, and then the meshgrid is called to generate the 2d matrices, needed by matplotlib to make its calculations.
• Lines 59 to 70 read the input file data and calculates the levels inside it, from the interval and the offset. Since calculating isobands for levels not present in the file isn't efficient, the minimum and maximum values in the input file are calculated before the isobands.
• The line 72 is where the isobands are actually calculated using the contourf function.
•  Lines 76 to 105 create the polygons at the output vector file.
• The generated contour has a property called collections, containing every isoband.
• Each element in the collections has the paths of the isolines.
• The property codes in the path indicates if a new ring has to be generated.
• The other lines are to generate an OGR feature 

isobands_gdal.py

This script is quite dirtier, since I have used a trick to get the isobands from the ContourGenerate function.

Closing the contour lines, which is what has to be done to transform isolines to isobands, is not an easy task.

Looking at some D3js examples I got the idea from Jason Davies conrec.js. I can't find the original example now, but basicaly, the idea is to add some pixels around the image with a value lower than the lowest value, so all the isolines will be closed. The solution gets closer, but some problems must be solved:

• Convert the isolines to polygons
• Clip the vectors to the original extent
• Substract the overlapping polygons, since when the lines are converted to polygons, all the area above the isoline value is contained in the polygon even though other lines with higher values are inside

When not clipped, the isolines will create strange effects at the borders

The main part code is exacly the same as in the other script, and the isobands function is:

def isobands(in_file, band, out_file, out_format, layer_name, attr_name, 
    offset, interval, min_level = None):
    '''
    The method that calculates the isobands
    '''    
    #Loading the raster file
    ds_in = gdal.Open(in_file)
    band_in = ds_in.GetRasterBand(band)
    xsize_in = band_in.XSize
    ysize_in = band_in.YSize

    stats = band_in.GetStatistics(True, True)
    
    if min_level == None:
        min_value = stats[0]
        min_level = ( offset + interval * 
            (floor((min_value - offset)/interval) - 1) )
    nodata_value = min_level - interval    



    geotransform_in = ds_in.GetGeoTransform()
    
    srs = osr.SpatialReference()
    srs.ImportFromWkt( ds_in.GetProjectionRef() )  

    data_in = band_in.ReadAsArray(0, 0, xsize_in, ysize_in)


    #The contour memory
    contour_ds = ogr.GetDriverByName('Memory').CreateDataSource('')
    contour_lyr = contour_ds.CreateLayer('contour', 
        geom_type = ogr.wkbLineString25D, srs = srs )
    field_defn = ogr.FieldDefn('ID', ogr.OFTInteger)
    contour_lyr.CreateField(field_defn)
    field_defn = ogr.FieldDefn('elev', ogr.OFTReal)
    contour_lyr.CreateField(field_defn)

    #The in memory raster band, with new borders to close all the polygons
    driver = gdal.GetDriverByName( 'MEM' )
    xsize_out = xsize_in + 2
    ysize_out = ysize_in + 2

    column = numpy.ones((ysize_in, 1)) * nodata_value
    line = numpy.ones((1, xsize_out)) * nodata_value

    data_out = numpy.concatenate((column, data_in, column), axis=1)
    data_out = numpy.concatenate((line, data_out, line), axis=0)

    ds_mem = driver.Create( '', xsize_out, ysize_out, 1, band_in.DataType)
    ds_mem.GetRasterBand(1).WriteArray(data_out, 0, 0)
    ds_mem.SetProjection(ds_in.GetProjection())
    #We have added the buffer!
    ds_mem.SetGeoTransform((geotransform_in[0]-geotransform_in[1],
        geotransform_in[1], 0, geotransform_in[3]-geotransform_in[5], 
        0, geotransform_in[5]))
    gdal.ContourGenerate(ds_mem.GetRasterBand(1), interval, 
        offset, [], 0, 0, contour_lyr, 0, 1)

    #Creating the output vectorial file
    drv = ogr.GetDriverByName(out_format)
    if exists(out_file):
        remove(out_file)
    dst_ds = drv.CreateDataSource( out_file )

      
    dst_layer = dst_ds.CreateLayer(layer_name, 
        geom_type = ogr.wkbPolygon, srs = srs)

    fdef = ogr.FieldDefn( attr_name, ogr.OFTReal )
    dst_layer.CreateField( fdef )


    contour_lyr.ResetReading()

    geometry_list = {}
    for feat_in in contour_lyr:
        value = feat_in.GetFieldAsDouble(1)

        geom_in = feat_in.GetGeometryRef()
        points = geom_in.GetPoints()

        if ( (value >= min_level and points[0][0] == points[-1][0]) and 
            (points[0][1] == points[-1][1]) ):
            if (value in geometry_list) is False:
                geometry_list[value] = []

            pol = ogr.Geometry(ogr.wkbPolygon)
            ring = ogr.Geometry(ogr.wkbLinearRing)

            for point in points:

                p_y = point[1]
                p_x = point[0]
                          
                if p_x < (geotransform_in[0] + 0.5*geotransform_in[1]):
                    p_x = geotransform_in[0] + 0.5*geotransform_in[1]
                elif p_x > ( (geotransform_in[0] + 
                    (xsize_in - 0.5)*geotransform_in[1]) ):
                    p_x = ( geotransform_in[0] + 
                        (xsize_in - 0.5)*geotransform_in[1] )
                if p_y > (geotransform_in[3] + 0.5*geotransform_in[5]):
                    p_y = geotransform_in[3] + 0.5*geotransform_in[5]
                elif p_y < ( (geotransform_in[3] + 
                    (ysize_in - 0.5)*geotransform_in[5]) ):
                    p_y = ( geotransform_in[3] + 
                        (ysize_in - 0.5)*geotransform_in[5] )

                ring.AddPoint_2D(p_x, p_y)
                
  
            pol.AddGeometry(ring)
            geometry_list[value].append(pol)



    values = sorted(geometry_list.keys())

    geometry_list2 = {}

    for i in range(len(values)):
        geometry_list2[values[i]] = []
        interior_rings = []
        for j in range(len(geometry_list[values[i]])):
            if (j in interior_rings) == False:
                geom = geometry_list[values[i]][j]
                
                for k in range(len(geometry_list[values[i]])):
                    
                    if ((k in interior_rings) == False and 
                        (j in interior_rings) == False):
                        geom2 = geometry_list[values[i]][k]
                        
                        if j != k and geom2 != None and geom != None:
                            if geom2.Within(geom) == True:
                                
                                geom3 = geom.Difference(geom2)
                                interior_rings.append(k)
                                geometry_list[values[i]][j] = geom3
                                                            
                            elif geom.Within(geom2) == True:
                                
                                geom3 = geom2.Difference(geom)
                                interior_rings.append(j)
                                geometry_list[values[i]][k] = geom3
                    
        for j in range(len(geometry_list[values[i]])):
            if ( (j in interior_rings) == False and 
                geometry_list[values[i]][j] != None ):
                geometry_list2[values[i]].append(geometry_list[values[i]][j])
    

    for i in range(len(values)):
        value = values[i]
        if value >= min_level:
            for geom in geometry_list2[values[i]]:
                
                if i < len(values)-1:

                    for geom2 in geometry_list2[values[i+1]]:
                        if geom.Intersects(geom2) is True:
                            geom = geom.Difference(geom2)
                
                feat_out = ogr.Feature( dst_layer.GetLayerDefn())
                feat_out.SetField( attr_name, value )
                feat_out.SetGeometry(geom)
                if dst_layer.CreateFeature(feat_out) != 0:
                    print "Failed to create feature in shapefile.\n"
                    exit( 1 )
                feat_out.Destroy()

• Lines 23 to 44 read the input file, including the data, geotransform, etc.
• Lines 47 to 54 create a vector file where the contour lines will be written. Since the data must be clipped later, the file is a temporary memory file.
• Lines 56 to 71 create a memory raster  file with the input data, plus a buffer around it with a value lower than the lowest in the input data, so the contour lines will get closed.
• Line 74 calls the ContourGenerate function, that will add the contour lines to the vectorial memory file.
• Lines 77 to 91 create the actual output file
• Lines 93 to 130 create a collection of geometries with the polygons.
• The lines are transformed to polygons by creating a ring from the polyline and adding it to a polygon.
• Lines 113 to 123 clip the polygons to the original geotransform, by moving the coordinates of the points outside the geotransform to the border.
• Lines 138 to 167 stores the difference from the polygons that overlap, so the output polygons contain only the zones where the values are in the interval.
• Lines 170 to 187 write the final polygons to the output file, the same way than the other script.

Notes:

An other option would be, of course, creating the polygons myself. I tried to do it, but as you can see at the marching squares wikipedia page, the algorithm is not easy when using polygons, and especially the matplotlib version of the scripts is quite clean.

The scripts have a problem when there is a nodata zone, since I haven't added the code to handle it.

Finally, as asked in the GDAL-dev mailing list, the best option would be modifying the ContourGenerate function to create isobands, but I think that is out of my scope.
The discussion at the GDAL-dev mailing list where I posted the first version. 

 

The data used for the examples is the same I used at the raster classification post.

 

Some links I have used:
http://matplotlib.org/api/path_api.html
http://matplotlib.org/api/pyplot_api.html#matplotlib.pyplot.contourf
http://matplotlib.org/basemap/api/basemap_api.html#mpl_toolkits.basemap.Basemap.contourf
http://fossies.org/dox/matplotlib-1.2.0/classmatplotlib_1_1contour_1_1QuadContourSet.html

Creating a grid from scattered data using inverse of the distance with python (gdal_grid approach)

OK, I have to admit that I was so happy when I found the  scipy rbf function that I went too fast writing the entry about inverse of the distance.
I swear that the images are real (you can check it yourself), but when you change a few parameters or the point position, the result is really strange, definitely not the inverse of the distance algorithm I was thinking about.
Looking a little more around the gdal documentation, I found this explanation, which is very easy and clear:
http://www.gdal.org/grid_tutorial.html
The problem is that, at least in my python gdal version, is not possible to call the function directly, so I've been coding a little to get it.
All the example code and files can be downloaded in a zip file.

First version: the algorithm

Putting all the code directly makes things difficult to understand, so first,  I'll reproduce the same program I wanted to show in the entrance, using matplotlib to show the results:

from math import pow
from math import sqrt
import numpy as np
import matplotlib.pyplot as plt

def pointValue(x,y,power,smoothing,xv,yv,values):
    nominator=0
    denominator=0
    for i in range(0,len(values)):
        dist = sqrt((x-xv[i])*(x-xv[i])+(y-yv[i])*(y-yv[i])+smoothing*smoothing);
        #If the point is really close to one of the data points, return the data point value to avoid singularities
        if(dist<0.0000000001):
            return values[i]
        nominator=nominator+(values[i]/pow(dist,power))
        denominator=denominator+(1/pow(dist,power))
    #Return NODATA if the denominator is zero
    if denominator > 0:
        value = nominator/denominator
    else:
        value = -9999
    return value

def invDist(xv,yv,values,xsize=100,ysize=100,power=2,smoothing=0):
    valuesGrid = np.zeros((ysize,xsize))
    for x in range(0,xsize):
        for y in range(0,ysize):
            valuesGrid[y][x] = pointValue(x,y,power,smoothing,xv,yv,values)
    return valuesGrid
    

if __name__ == "__main__":
    power=1
    smoothing=20

    #Creating some data, with each coodinate and the values stored in separated lists
    xv = [10,60,40,70,10,50,20,70,30,60]
    yv = [10,20,30,30,40,50,60,70,80,90]
    values = [1,2,2,3,4,6,7,7,8,10]
    
    #Creating the output grid (100x100, in the example)
    ti = np.linspace(0, 100, 100)
    XI, YI = np.meshgrid(ti, ti)

    #Creating the interpolation function and populating the output matrix value
    ZI = invDist(xv,yv,values,100,100,power,smoothing)


    # Plotting the result
    n = plt.normalize(0.0, 100.0)
    plt.subplot(1, 1, 1)
    plt.pcolor(XI, YI, ZI)
    plt.scatter(xv, yv, 100, values)
    plt.title('Inv dist interpolation - power: ' + str(power) + ' smoothing: ' + str(smoothing))
    plt.xlim(0, 100)
    plt.ylim(0, 100)
    plt.colorbar()

    plt.show()
    

Let's explain it step by step:

1. The main method defines some sample data, calls the interpolation function and draws it using matplotlib. Just copy&paste, since it's long to explain.
2. invDist function: For each point in the coordinates matrix, a value needs to be calculated. First, a xSize*ySize zeroes values is calculated. Then for each point coordinate (the pixel position, in this simple case), a function that calculates the value is called.
3. This is the important part: We apply the formula: $V=\frac{\sum\limits_{i=1}^n \frac{v_{i}}{d_{i}^{p}}}{\sum\limits_{i=1}^n \frac{1}{d_{i}^{p}}}$ for each pixel.
   
   • V is the interpolated value. 
   • n is the number of points
   • d is the distance from the point to the pixel
   • v is the value of the point
   • p is the power we want to apply to the distance o weight it.
   The distance is the Cartesian one, plus the smoothing factor (it gives more distance than the actual one, lowering the influence around the points). If the distance is close to the precision of the float numbers, we give the data value instead of the interpolated one, to avoid strange results.

And that's all. Here, the results (you can compare them with the ones in the other entry) which are consistent to the inverse of the distance method:

 If the smoothing is zero and the power is high, the interpolation changes a lot around the points to give them their exact value.

If the smoothing is high and the power is one, the result is much smoother, but the values at the points are not maintained.

Adding the GIS stuff:

The example above doesn't write to a GIS file. The function invDist must be changed so it creates the file using a gdal driver:

def invDist(xv,yv,values,geotransform,proj,xSize,ySize,power,smoothing,driverName,outFile):
    #Transform geographic coordinates to pixels
    for i in range(0,len(xv)):
         xv[i] = (xv[i]-geotransform[0])/geotransform[1]
    for i in range(0,len(yv)):
         yv[i] = (yv[i]-geotransform[3])/geotransform[5]
    #Creating the file
    driver = gdal.GetDriverByName( driverName )
    ds = driver.Create( outFile, xSize, ySize, 1, gdal.GDT_Float32)
    if proj is not None:
        ds.SetProjection(proj.ExportToWkt())
    ds.SetGeoTransform(geotransform)
    valuesGrid = np.zeros((ySize,xSize))
    #Getting the interpolated values
    for x in range(0,xSize):
        for y in range(0,ySize):
            valuesGrid[y][x] = pointValue(x,y,power,smoothing,xv,yv,values)
    
    ds.GetRasterBand(1).WriteArray(valuesGrid)
    ds = None
    return valuesGrid

1. Note that the function will  need the geographic parameters geotransform and proj, as well as the output file name and driver.
2. First, the point positions must be changed to pixel locations in order to calculate distances
3. Then, the output file is created with the size and projection asked by the user
4. The values are calculated in the same way as in the other example
5. The file is written

The data in the first example was set into three lists, but the correct way to do it would be read it from a geometry file with the OGR library. Another function is defined to do that:

def readPoints(dataFile,Zfield='Z'):
    data = {}
    xv=[]
    yv=[]
    values=[]
    ds = ogr.Open(dataFile)
    if ds is None:
       raise Exception('Could not open ' + dataFile)
    
    layer = ds.GetLayer()
    proj = layer.GetSpatialRef()
    extent = layer.GetExtent()

    feature = layer.GetNextFeature()
    if feature.GetFieldIndex(zField) == -1:
         raise Exception('zField is not valid: ' + zField)

    while feature:
        geometry = feature.GetGeometryRef()
        xv.append(geometry.GetX())
        yv.append(geometry.GetY())
        values.append(feature.GetField(zField))

        feature = layer.GetNextFeature()
    data['extent'] = extent 
    data['xv']=xv
    data['yv']=yv
    data['values']=values
    data['proj'] = proj
    ds = None
    return data

1. The function reads the point position and values from the given file and field name.
2. A dictionary is returned, to help retrieving all the values we may need to create the output raster. If no projection or geotransform is passed by the user, the input file extents and projection are used.
3. In the example files, a file called points.shp has some sample points to test the functions.

Finally, the main method must get the  parameters from the user, and call the other two methods to create the raster. I have copied some of the input options from the gdal_grid program, so it's easier to test the results. Of course, not all the options are implemented, but it shouldn't be difficult to do it.

if __name__ == "__main__":
    #Setting the default values
    power=2
    smoothing=0
    
    zField='Z'
    dataFile=None
    outFile=None
    driverName='GTiff'
    proj=None

    geotransform = None
    xMin=None
    xMax=None
    yMin=None
    yMax=None
    xSize=100
    ySize=100

    #Parsing the command line
    argv = gdal.GeneralCmdLineProcessor( sys.argv )
    
    i = 1
    while i < len(argv):
        arg = argv[i]
        if arg == '-out_format':
         driverName = argv[i+1]
         driverName = driverName.replace("'","")
         driverName = driverName.replace('"','')
         i = i + 1
        elif arg == '-zfield':
         zField = argv[i+1]
         zField = zField.replace("'","")
         zField = zField.replace('"','')
         i = i + 1
        elif arg == '-a_srs':
         proj = argv[i+1]
         proj = proj.replace("'","")
         proj = proj.replace('"','')
         i = i + 1
        elif arg == '-outsize':
         xSize = argv[i+1]
         xSize = xSize.replace("'","")
         xSize = int(xSize.replace('"',''))
         ySize = argv[i+2]
         ySize = ySize.replace("'","")
         ySize = int(ySize.replace('"',''))
         i = i + 2
        elif arg == '-txe':
         xMin = argv[i+1]
         xMin = xMin.replace("'","")
         xMin = float(xMin.replace('"',''))
         xMax = argv[i+2]
         xMax = xMax.replace("'","")
         xMax = float(xMax.replace('"',''))
         i = i + 2
        elif arg == '-tye':
         yMin = argv[i+1]
         yMin = yMin.replace("'","")
         yMin = float(yMin.replace('"',''))
         yMax = argv[i+2]
         yMax = yMax.replace("'","")
         yMax = float(yMax.replace('"',''))
         i = i + 2
        elif dataFile is None:
         dataFile = arg
         dataFile = dataFile.replace("'","")
         dataFile = dataFile.replace('"','')
        elif outFile is None:
         outFile = arg
         outFile = outFile.replace("'","")
         outFile = outFile.replace('"','')
        i = i + 1



    if dataFile is None or outFile is None:
        usage()
    try:
        data = readPoints(dataFile,zField)
    except Exception,ex:
        print ex
        sys.exit(0)
    if xMin is None:
        xMin=data['extent'][0]
        xMax=data['extent'][1]
    if yMin is None:
        yMin=data['extent'][2]
        yMax=data['extent'][3]

    geotransform=[]
    geotransform.append(xMin)
    geotransform.append((xMax-xMin)/xSize)
    geotransform.append(0)
    geotransform.append(yMax)
    geotransform.append(0)
    geotransform.append((yMin-yMax)/ySize)

    if proj is None:
        proj = data['proj'] 
    else:
        try:
            proj = osr.SpatialReference()
            proj.SetFromUserInput(str(proj))  
        except Exception,ex:
            print ex 
            sys.exit(0)
    #Creating the interpolation function and populating the output matrix value
    try:
        ZI = invDist(data['xv'],data['yv'],data['values'],geotransform,proj,xSize,ySize,power,smoothing,driverName,outFile)
    except Exception,ex:
        print ex
        sys.exit(0)

1. First, the default parameter values are set. Some of them are None, since they are mandatory.
2. Then, the input arguments are read.
3. After having the input arguments, all the parameters that can be set, are set.
4. The function that reads the input file is run, and with it's result, the raster is created. Note that the geotransform is defined from the input file if no one is set by the user.

And the result is something like this when opened with QGis or any GIS:

The points are not coloured, but are the ones in the original file.
The whole code comes in the example file, with all the data you need to run the example.
To generate the picture above, the command is:
 python invdistgis.py -zfield value points.shp out.tiff

What's next

The original gdal_grid implements more interpolation methods (nearest value, and average). Doing the same in the script is as easy as adding other functions to use instead of pointValue.

Also, in the original program, an ellipse can be set to search only in some area around each pixel. This would be a little more difficult do implement, but is easy to find it in the gdal source code in a file called gdalgrid.cpp. I've put it in the example data.

As you can see, implementing this kind of stuff in python is not as difficult as it may seem at the beginning.