Since I work at a meteorological service I have to deal quite often with
numerical weather prediction models. I use to work with GRIB files that have the data in the format I need to draw simple maps.
But sometimes, I need to calculate stuff that require the original data, since GRIB files are usually reprojected and simplified in vertical levels.
In the case of the
WRF model, the output is in NetCDF format. The data is in sigma levels instead the pressure levels I need, and the variables such as temperature don't come directly in the file, but need to be calculated.
The post is actually written to order the things I've been using for myself, but I've added it to the blog because I haven't found step by step instructions.
Getting the data
I have used some data from the model run at the
SMC, where I work, but you can get a WRF output
from the ucar.edu web site. The projection is different from the one I have used, and it has 300 sigma levels instead of 30, but it should work.
The NetCDF format
Every NETCDF file contains a collection of datasets with different sizes and types. Each dataset can have one or more layers, can have unidimensional arrays in it, etc. So the "traditional" GDAL datamodel can't work directly, since assumes that a file have multiple layers of the same size. That's why "subdatasets" are introduced. So opening the file directly (or running gdalinfo) only gives some metadata about all the datasets, but no actual data can be read or consulted. To do it, the subdataset must be opened instead.
Opening a subdataset
Since opening the file directly doesn't open the actual dataset, but the "container", a different notation is used, maintaining the Open method. The filename string must be preceded by NETCDF: and continued by :VAR_NAME
To open the variable XLONG subdataset, the order would be:
gdal.Open('NETCDF:"'+datafile+'":XLONG')
ARWPost
ARWPost is a program that reads WRF outputs in FORTRAN. I have used it's code to know how to calculate the actual model variables from the model NetCDF file.
There is a file for calculating each variable, some for the interpolation, etc. so it has helped me a lot when trying to understand how everything works.
The problem of ARWPost is that the usage is quite complicated (change a configuration file and executing), so it was not very practical to me.
Sigma Levels
Instead of using constant pressure levels, the wrf model works using the
Sigma coordinate system
This makes a bit more difficult extracting the data at a constant pressure, since for every point in the horizontal grid, a different level position is needed to get the value.
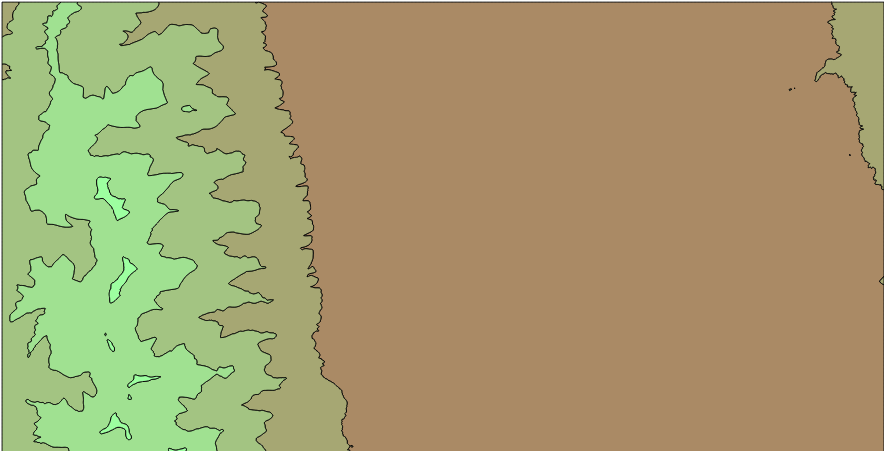
Besides, not all the variables use the same sigma levels. There are two different level sets known as "half levels" and "full levels", as shown in the picture:
Of course, this makes things a bit more complicated.
A layer sigma value in the half level is the average between full level above and below.
Getting the geopotential height at a pressure level, step by step
Setting the right projection
NetCDF
can hold the following projections:
'lambert', 'polar', 'mercator', 'lat-lon' and 'rotated_ll'. The projection is defined using the label MAP_PROJ at the original file metadata (not the subdatasets metadata). To get all the metadata file, jut use:
ds_in = gdal.Open(datafile)
metadata = ds_in.GetMetadata()
All the metadata comes with the prefix NC_GLOBAL#
In my case, I have MAP_PROJ=2 ,so the projection is polar stereographic (the code is the position in the projection list, starting by 1). I'll set it with:
proj_out = osr.SpatialReference()
proj_out.SetPS(90, -1.5, 1, 0, 0)
where -1.5 is the STAND_LON label at the original file metadata and 90 is the POLE_LAT label.
Finding the geotransform
I'm not sure if the method I use is the best one, but the data I get is consistent.
The metadata given at the main file doesn't set the geotransform properly (or, at least, I'm not able to get it), since it sets only the center point coordinates, and the deltax and deltay. But this deltas are not referenced to the same point, so getting the real geotransform is not easy.
Fortunately, the files come with the fields XLONG and XLAT, that contain the longitude and latitude for each point in the matrix. So taking the corners is possible to get the geotransform, although the coordinates have to be reprojected before:
ds_lon = gdal.Open('NETCDF:"'+datafile+'":XLONG')
ds_lat = gdal.Open('NETCDF:"'+datafile+'":XLAT')
longs = ds_lon.GetRasterBand(1).ReadAsArray()
lats = ds_lat.GetRasterBand(1).ReadAsArray()
ds_lon = None
ds_lat = None
proj_gcp = osr.SpatialReference()
proj_gcp.ImportFromEPSG(4326)
transf = osr.CoordinateTransformation(proj_gcp, proj_out)
ul = transf.TransformPoint(float(longs[0][0]), float(lats[0][0]))
lr = transf.TransformPoint(float(longs[len(longs)-1][len(longs[0])-1]), float(lats[len(longs)-1][len(longs[0])-1]))
ur = transf.TransformPoint(float(longs[0][len(longs[0])-1]), float(lats[0][len(longs[0])-1]))
ll = transf.TransformPoint(float(longs[len(longs)-1][0]), float(lats[len(longs)-1][0]))
gt0 = ul[0]
gt1 = (ur[0] - gt0) / len(longs[0])
gt2 = (lr[0] - gt0 - gt1*len(longs[0])) / len(longs)
gt3 = ul[1]
gt5 = (ll[1] - gt3) / len(longs)
gt4 = (lr[1] - gt3 - gt5*len(longs) ) / len(longs[0])
geotransform = (gt0,gt1,gt2,gt3,gt4,gt5)
Getting the geopotential height
From the ARWPost code, I know that the geopotential height is:
H = (PH + PHB)/9.81
So the PH and PHB subdatasets must be added and divided by the gravity to get the actual geopotential height
The code:
ds_ph = gdal.Open('NETCDF:"'+datafile+'":PH')
ds_phb = gdal.Open('NETCDF:"'+datafile+'":PHB')
num_bands = ds_ph.RasterCount
data_hgp = numpy.zeros(((num_bands, ds_ph.RasterYSize, ds_ph.RasterXSize)))
for i in range(num_bands):
data_hgp[i,:,:] = ( ds_ph.GetRasterBand(num_bands - i).ReadAsArray() + ds_phb.GetRasterBand(num_bands - i).ReadAsArray() ) / 9.81
ds_ph = None
ds_phb = None
Note that the bands are inverted in order and that in the raster, the order of the elements is [layer][y][x]. This is needed later to calculate layer positions.
Calculating the geopotential height for a given Air Pressure
At this moment, we have the geopotential height for every sigma level, which is not very useful for working with the data. People prefers to have the geopotential height for a given pressure (850 hPa, 500 hPa, and so on).
The model gives the pressure values at every point, calculated doing:
Press = P + PB
in Pa or
Press = (P + PB ) / 100
in hPa
The code for reading the pressure:
ds_p = gdal.Open('NETCDF:"'+datafile+'":P')
ds_pb = gdal.Open('NETCDF:"'+datafile+'":PB')
num_bands = ds_p.RasterCount
data_p = numpy.zeros(((num_bands, y_size, x_size)))
for i in range(num_bands):
data_p[i,:,:] = ( ds_p.GetRasterBand(num_bands - i).ReadAsArray() + ds_pb.GetRasterBand(num_bands - i).ReadAsArray() ) / 100
ds_p = None
ds_pb = None
Now we can calculated at which layer on the pressure subdataset the given pressure would be.
NumPy has a function that calculates at which position a value would be in an ordered array called searchsorted: http://docs.scipy.org/doc/numpy/reference/generated/numpy.searchsorted.html
numpy.searchsorted([1,2,3,4,5], 2.5)
would give
2, since the value 2.5 is between 2 and 3 (positions 1 and 2).
I needed two tricks to use it:
*The function needs to have an ascending ordered array. That's why the layers order is reversed in the code, because the air pressure is descending with height, and we need the opposite to use this function.
*The function can only run in 1-d arrays. To use it in our 3-d array, the numpy.apply_along_axis function is used:
numpy.apply_along_axis(lambda a: a.searchsorted(p_ref), axis = 0, arr = data_p)
where p_ref is the pressure we want for the geopotential height.
That's why the layer number is the first element in the array, because is the only way to get apply_along_axis work.
The final code for the calculation:
p_ref = 500
data_positions = numpy.apply_along_axis(lambda a: a.searchsorted(p_ref), axis = 0, arr = data_p)
Now we know between which layers a given pressure would be for every point. To know the actual pressures at the upper and lower level for each point, the numpy.choose function can be used:
p0 = numpy.choose(data_positions - 1, data_p)
p1 = numpy.choose(data_positions, data_p)
layer_p = (data_positions - 1) + (p_ref - p0) / (p1 - p0)
Now we know the position in the pressure layers. i.e. if we want 850 hPa, ant for one point the upper layer 3 is 900 hPa and the lower layer 2 is 800 hPa, the value would be 2.5
But for the geopotential height, the sigma level is not the same, since the pressure is referenced to the half levels, and the geopotential to the full levels.
So the we will add 0.5 layers to the pressure layer to get the geopotential height layer:
layer_h = layer_p + 0.5
Then the final value will be:
h0 = numpy.floor(layer_h).astype(int)
h1 = numpy.ceil(layer_h).astype(int)
data_out = ( numpy.choose(h0, data_hgp) * (h1 - layer_h) ) + ( numpy.choose(h1, data_hgp) * (layer_h - h0) )
Note that the h0 and h1 (the positions of the layers above and below the final position) must be integers to be used with the choose function.
Extrapolation
If the wanted pressure is 500hPa, a data layer above and below will be always found. But when we get closer to the land, like at 850 hPa, another typical pressure to show the geopotential height, we find that in some points, the pressure value is above the pressure layers of the model. So an extrapolation is needed, and the previous code, that assumed that the value would always between two layers will fail.
So the data calculated above must be filtered for each case. For the non interpolated data:
data_out = data_out * (data_positions < num_bands_p)
The extrapolation is defined in the file module_interp.f90 from the ARWPost source code. There are two defined cases:
- The height is below the lowest sigma level, but above the ground height defined for that point
- The height is below the ground level
The first case is quite simple, because the surface data for many variables is available, so it only changes the layer used to calculate the interpolation:
##If the pressure is between the surface pressure and the lowest layer
array_filter = numpy.logical_and(data_positions == num_bands_p, p_ref*100 < data_psfc)
zlev = ( ( (100.*p_ref - 100*data_p[-1,:,:])*data_hgt + (data_psfc - 100.*p_ref)*data_hgp[-1,:,:] ) / (data_psfc - 100*data_p[-1,:,:]))
data_out = data_out + (zlev * array_filter )
The second case needs to extrapolate below the ground level. The code at the file module_interp.f90 iterates over each element in the array, but using numpy will increase the speed a lot, so let's see how is it done:
expon=287.04*0.0065/9.81
ptarget = (data_psfc*0.01) - 150.0
kupper = numpy.apply_along_axis(lambda a: numpy.where(a == numpy.min(a))[0][0] + 1, axis = 0, arr = numpy.absolute(data_p - ptarget))
pbot=numpy.maximum(100*data_p[-1,:,:], data_psfc)
zbot=numpy.minimum(data_hgp[-1,:,:], data_hgt)
tbotextrap=numpy.choose(kupper, data_tk) * pow((pbot/(100*numpy.choose(kupper, data_p))),expon)
tvbotextrap=tbotextrap*(0.622+data_qv[-1,:,:])/(0.622*(1+data_qv[-1,:,:]))
zlev = zbot+((tvbotextrap/0.0065)*(1.0-pow(100.0*p_ref/pbot,expon)))
data_out = data_out + ( zlev * array_filter )
- Expon and ptarget are calculated directly (ptarget is an array, but the operations are simple)
- kupper is a parameter that could be defined as the level where the absolute value of the pressure - ptarget changes. Since we have a 3d array, being the 0th dimension the level, we can calculate the values in the 2d xy matrix by using the apply_along_axis method. This method will take all the levels and run the function defined in the first parameter passing the second parameter as the argument. In our case, the position (where) of the minimum value (min). We add the +1 to get the same result than the original code.
So in one line, we do what in the original code needs three nested loops!
The value is inverse to the ones at the original code, because we changed the pressure order.
- pbot and zbot are only to take the value closer to the ground betweeen the lowest level and the ground level defined by the model
- tbotextrap is the extrapolated temperature. The choose function is used to get the value at the calculated kupper level for each element in the matrix.
- tvbotextrap is the virtual temperature for tbotextrap. The original code uses an external function, but I have joined everything. The formula for the virtual temperature is virtual=tmp*(0.622+rmix)/(0.622*(1.+rmix))
- zlev can be calculated directly with the values calculated before, and is added to the output after applying the filter.
Drawing the map using Basemap
The output file can be opened with QGIS, or any other GIS capable to read GeoTIFF files.
But is possible to draw it directly from the script using Basemap:
from mpl_toolkits.basemap import Basemap
import matplotlib.pyplot as plt
m = Basemap(projection='cyl',llcrnrlat=40.5,urcrnrlat=43,\
llcrnrlon=0,urcrnrlon=3.5,resolution='h')
cs = m.contourf(longs,lats,data_out,numpy.arange(1530,1600,10),latlon=True)
m.drawcoastlines(color='gray')
m.drawcountries(color='gray')
cbar = m.colorbar(cs,location='bottom',pad="5%")
cbar.set_label('m')
plt.title('Geopotential height at 850hPa')
plt.show()
- First, we initialize the projection (latlon directly in this case), setting the map limits.
- contourf will draw the isobands for each 10m.
- Then, just draw the borders and coas lines and show the map.
This is how the map at the header was made.
Notes
To compile ARWPost in my Ubuntu, the file src/Makefile needs to be changed: -lnetcdf for -lnetcdff
It was very hard for me to find it!